INFO4 - S8 - ID - Systèmes de raisonnement probabiliste (ID)
Aperçu des sections
-
La représentation des connaissances et le raisonnement à partir de ces représentations a donné naissance à de nombreux modèles. Les modèles graphiques probabilistes, et plus précisément les réseaux bayésiens (RB), initiés par Judea Pearl dans les années 1980 sous le nom de systèmes experts probabilistes, se sont révélés des outils très pratiques pour la représentation de connaissances incertaines et le raisonnement à partir d’informations incomplètes, dans de nombreux domaines comme la bio-informatique, la gestion du risque, le marketing, la sécurité informatique, le transport, etc.
Le but de ce cours est
- de définir la notion de réseau bayésien et de raisonnement probabiliste,
- de donner un aperçu des différents algorithmes permettant d'effectuer ce raisonnement (ou inférence) probabiliste,
- d'introduire la notion de construction automatique de ces modèles de raisonnement à partir de données.
- de présenter les extensions dynamiques et relationnelles de ces modèles.
The need of representating knowledge and reasoning from these representations has resulted in many models. Probabilistic graphical models, and more precisely Bayesian networks (BNs), initiated by Judea Pearl in the 1980s under the name of probabilistic expert systems, have proven to be very practical tools for representing uncertain knowledge and reasoning from incomplete information, in many fields such as bioinformatics, risk management, marketing, computer security, transportation, etc.
The goal of this course is- to define the notion of Bayesian network and probabilistic reasoning,
- to give an overview of the different algorithms allowing to perform this probabilistic reasoning (or inference),
- to introduce the notion of automatic construction/learning of these models from data,
- to present the dynamic and relational extensions of these models.
- de définir la notion de réseau bayésien et de raisonnement probabiliste,
-
- Lecture : slides part I - 2-5
- Assignments
- Please, fill the following document (Student statistics).
- Once the document will be complete, estimate the following distributions:
- P(Gl, Re, Ta, Lo) [from the statistics gathered] This is a joint distribution, check that its sum is one.
- P(Gl, Re, Ta) [marginalization] This is another joint distribution summing to one
- P(Lo | Gl, Re, Ta) [definition of conditional probability distribution] This is a
conditional distribution, which is a set of joint distributions (one for
each value of {GL, Re, Ta}, so you can check that each joint distribution
sums to one.
- et ainsi de suite pour P(Gl, Re), P(Ta | Gl, Re), P(Gl) et P(Re | Gl)
- P(Gl, Re, Ta, Lo) [from the statistics gathered] This is a joint distribution, check that its sum is one.
- Finally, choose one configuration (set of values) for {Gl, Re, Ta, Lo} and check for this configuration that P(Gl, Re, Ta, Lo) = P(Gl) * P(Re | Gl) * P(Ta | Gl, Re) * P(Lo | Gl, Re, Ta) [chain rule]
- Let's imagine that Re and Gl are independent, and that Lo is independent
with Re and Ta given Gl. What would be the simplification of the chain
rule decomposition by adding such assumptions ?
- Please, fill the following document (Student statistics).
-
2-3 - Définition - modèle de dépendances/indépendances / Bayesian network definition - dependence modelling
- Lecture: slides part I - 7-17
- Assignments
- Let's consider 3 variables A, B and C, what directed acyclic graphs
encode the following assumptions ? Provide some realistic examples for
all these scenarios.
- A, B and C are all independent.
- A and B are "directly" dependent (they are dependent, and dependent conditionally to any other variable), B and C are independent, A and C are independent.
- A and B are "directly" dependent, B and C are "directly" dependent, A and C are dependent but independent given B.
- A and B are "directly" dependent, B and C are "directly" dependent, A and C are independent but dependent given B.
- Write the decomposition of the joint distribution as a product of local conditional distributions for the graph depicted below
- Markov Equivalence :
- definition : "inferred edges" are the arcs which are not members of a V-structure, but whose orientation is also constrained (if we inverted them, we could for example create a new V-structure not present in the original graph)
- Let us consider 3 variables. How many different DAGs with 3 variables exist? Which ones are Markov equivalent? And how many different CPDAGs exist with these 3 variables?
-
- Lecture: slides part I - 19-20
- cf slide 19
- implement your model in pyAgrum to answer to the following questions (you can check the answers with a simple logical reasoning)
- what is the probability of the reading in cell 2 equal to 0 (N2=0) i.e. you click in cell 2 and nothing happens : no bomb in cell 2 neither in its adjacent cells) ?
- what is the probability distribution of N2 if you observed that N1=0 ? if you observed that N1=0 and N3=1 ?
- what is the probability of N4 when N1=0 and N3=1 ?
- bonus questions :
- let us imagine that we know the total number of bombs in the grid. How to model this information in our BN. Add this in your Genie implementation and answer to the following questions :
- what is the probability of N2=0 if you know that there are 2 bombs in the grid ?
- what are the probability distributions of N2, N3 and N4 if you observed that N1=0 ?
- Lecture: slides part I - 19-20
-
- Lecture: slides part I - 21-25
- DAG : how can we recognize a tree ? a poly-tree ? Wikipedia
-
- (original file : Animals.xdsl)
- BN used during the course : Animals2.xdsl (generated by replacing logical dependencies by CPDs)
- Scenario 1 : without evidence
- initialization of λ vectors : ?
- first λ messages : λWa(Cl)= ? λBo(Cl)= ? λHa(Cl)= ? but also λEn(An)= ? λBe(An)= ?
- aggregation of some λ messages : λ(Cl)=?
- last λ messages : λCl(An)=?
- last aggregation : λ(An)=?
- initialization of π vectors ?
- first π messages : πEn(An)=? πCl(An)=? πBe(An)=?
- first π aggregations : π(En)=? π(Cl)=? π(Be)=?
- other π messages : πWa(Cl)=? πBo(Cl)=? πHa(Cl)=?
- last π aggregations : π(Wa)=? π(Bo)=? π(Ha)=?
- and finally, what is the probability of each variable given the (empty) evidence ? (check with pyAgrum)
- Scenario 2 : with evidence {Class=Mammal, Bears Young As=Eggs}
- initialization of λ vectors : ?
- first λ messages :
- λWa(Cl), λBo(Cl), λHa(Cl) are skipped because Cl is observed
- λEn(An)= ? λBe(An)= ? λCl(An)= ?
- aggregation : λ(An)=?
- initialization of π vectors ?
- first π messages :
- πCl(An) and πBe(An) are skipped because Cl is observed
- πEn(An)=?
- first π aggregation : π(En)
- other π messages : πWa(Cl)=? πBo(Cl)=? πHa(Cl)=? you can notice that the information about Be is not usefull here !
- last π aggregations : π(Wa)=? π(Bo)=? π(Ha)=?
- and finally, what is the probability of each variable given the (empty) evidence ? (check with pyAgrum)
- Scenario 3 : with evidence {Warm Blooded=true, Bears Young As=Eggs}
- do it by yourself :-)
- (original file : Animals.xdsl)
-
- Lecture : slides Part II 3-7
- Assignment: ?
-
- Lecture : slides part II - 9-14 (complete data)
- Assignment
- Let's use the data provided in the file example-parameter-learning-complete.csv (cf. below)
- The CPDs (conditional probability distributions) corresponding to this network are P(A), P(B|A), P(D), P(C | A, D).
- The contingency tables associated to these CPDs are N(A), N(B,A), N(D), N(C, A, D). Fill these tables by counting the number of corresponding events in the dataset.
- Maximum of likelihood : how can we estime
P(A) from N(A) ? P(D) from N(D) ? P(B|A) from N(B,A) ? P(C | A,D) from
N(C, A,D) ? What are the results ?
- Let's consider the following Dirichlet coefficient αA=[1 1], αD=[3 7], αBA=[1 1; 1 1], αCAD=[1 1 1 1; 1 1 1 1]. What are the CPDs estimation with Expectation a posteriori approach ?
- Lecture: slides part II - 15-17 (incomplete data)
- Assignment
- Let's use the data provided in the file example-parameter-learning-incomplete.csv (cf. below)
- How many of the 50 lines of data will we consider by applying Complete Case Analysis approach ?
- If we now consider Available Case Analysis approach, how many lines will we consider for the estimation of P(A) ? P(D) ? P(B | A) ?
- EM algorithm :
- initialize the parameters by applying (by hand) Available Case Analysis approach
- use pyAgrum to implement this network
- First E step :
- the first missing data is the first sample, with A=0, C=0, D=0 and B missing.
- use your pyAgrum implementation to ask your actual network (initialized with ACA) what is P(B | A=0, C=0, D=0).
- what are the contingency tables impacted by this missing value ?
- if B surely observed and equal to 0, N(B=0) would be increased by 1. if B surely observed and equal to 1, N(B=1) would be increased by 1. Here B is missing, but we have an estimation of its probability, so N(B=0) and N(B=1) will be increased by the respective probability of P(B=0| A=0, C=0, D=0) and P(B=1| A=0, C=0, D=0). Same reasoning for N(A,B) where two values are impacted: N(A=0, B=0) and N(A,0, B=1).
- First M step : apply Maximum of Likelihood estimation to estimate one new version for each of your CPDs, and update your BN
- And officially, you can repeat this until convergence :-)
- Lecture : slides part II - 9-14 (complete data)
-
- Lecture: slides part II - 21-35
- Assignment
- Scoring function slide 26
- MWST algorithm: slide 31
- Greedy search algorithm: slide 34
- Lecture: slides part II - 21-35
-
- Use PyAgrum to load the Sachs BN
- init
import pyAgrum as gum
import pyAgrum.lib.notebook as gnb
import pyAgrum.lib.bn_vs_bn as bnvsbn - example
bnTheo=gum.loadBN('sachs.xdsl')
EGTheo=gum.EssentialGraph(bnTheo)
gnb.sideBySide(bnTheo,EGTheo)
- init
- generate several datasets from the Sachs network, for instance 5 datasets for each of the sizes = 50, 500, 1000, 5000
- example
gum.generateSample(bnTheo, 500, "sample_sachs_500_1.csv",True)
- example
- for each dataset, you will be able to run at least two algorithms provided by pyAgrum
- .Greedy Hill Climbing, which is a score-based algorithm that returns one DAG
learner=gum.BNLearner("sample_sachs_500_1.csv",bnTheo) #using bn as template for variables
learner.useGreedyHillClimbing()
learner.useScoreAIC() # or useScoreBIC, useScoreBDeu
bnApp=learner.learnBN()
print("Learned in {0}ms".format(1000*learner.currentTime()))
EGApp=gum.EssentialGraph(bnApp)
gnb.sideBySide(bnApp,EGApp) - MIIC, which is a recent constraint-based algorithm that returns one essential grap
learner2=gum.BNLearner("sample_sachs_500_1.csv",bnTheo) #using bn as template for variables
learner2.useMIIC()
learner2.useNoCorrection()
EGApp=learner2.learnEssentialGraph()
print("Learned in {0}ms".format(1000*learner2.currentTime()))
gnb.sideBySide(EGTheo,EGApp)
- .Greedy Hill Climbing, which is a score-based algorithm that returns one DAG
- you can estimate the quality of the learnt model, by comparing its essential graph to the theoretical one
bncmp=bnvsbn.GraphicalBNComparator(bnApp,bnTheo)
bncmp.hamming()- where the hamming function returns 2 values :
- hamming : the Hamming distance between the skeletons
- structural hamming : the Hamming distance between the corresponding essential graphs
- questions :
- why are we repeating each experiment (for one data size) several times ?
- for one experiment, can you explain why it is "dangerous" to compare directly both DAGs ? and why comparing both essential graphs is meaningful ?
- plot the learning time and the structural Hamming distance with respect to the data size. What are your conclusions ?
- Use PyAgrum to load the Sachs BN
-
- Lecture: slides part IV - PRM
- Assignment
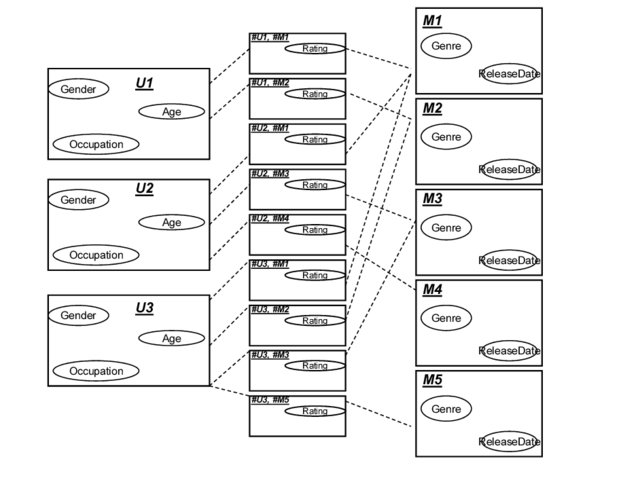
- complete the definition of the PRM described in the figure 1 given below (for need of simplicity, this model is absolutely unrealistic)
- Movie.Genre domain is [Drama, Horror, Comedy]
- Movie.ReleaseDate domain is [<2000, >=2000]
- User.Gender domain is [Male, Female]
- User.Age domain is [<10, 10-18, >18]
- User.Occupation domain is [student, working, retired]
- Vote.Rating domain is [Low, High]
- What CPDs are needed but not defined in fig.1 ?
- Use the instance of the database provided below to generate the corresponding Ground Bayesian Network
- Bonus question : "nightmare PRM" : one person's eye color depends on two
other person's eye color, the person who is the mother of the first
one, and the person who is his father. Model this sentence with the
simplest possible PRM.
- Lecture: slides part IV - PRM
-
How it works :
- one article per PERSON (and one person per article)
- make an analysis of the article: synthesis of the methods used, experiments, results, ... and your personal conclusions on the article
- registration : use the forum to post me (a msg from the delegate) the distribution of the articles, before March 25, 2024. Contact me at least ONE WEEK BEFORE if you want an article in a particular field.
- the report must be deposited on Madoc, in PDF format before April 19, 2024 - 19h